고정 헤더 영역
상세 컨텐츠
본문
이번 story에서는 Data Structure 중에서 Graph Data Structure에 대해서 이야기를 해보려고 한다. Graph Data Structure는 지도나 지하철노선, 전기회로 등에 이용될 수가 있다.
Graph Data Structure는 수학적인 모형들을 Data Structure로 표현할 수가 있다. 우선 아래의 그림을 통해서 수학적 모형을 확인해보면,
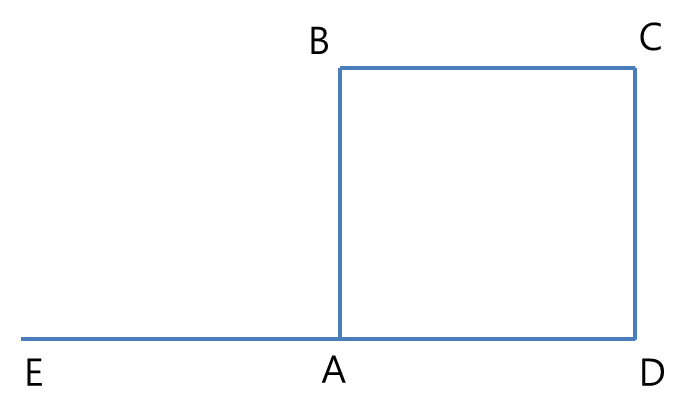
위의 그림을 보면, 각각의 꼭지점들(A, B, C, D, E)가 있고 그것들을 연결하는 모서리가 있다(AB, AD, AE, BC, CD)
Graph Data Structure 는 하나의 쌍(V, E)을 세트로 구성하고 있다.
V에는 각각의 정점들(vertices)의 노드정보들을 저장하고 있고 E에는 V에 들어가 있는 vertices들이 간선(edge)라고 하는 vertices들간의 연결에 대한 정보를 저장해 가지고 있다. 이를 통해서 객체들간의 연결관계를 나타내 거미줄과 유사한 그물망들을 만들어 낼 수가 있다. 또한 Graph Data Structure는 부분적으로 고립된 Graph Data Structure로 구성될 수도 있다.
Graph와 관련된 용어들을 살펴보면, 아래와 같은 용어들이 있다.
vertex(정점) : 위치를 나타낸다. (node)
edge(간선) : 정점들 간의 관계를 나타낸다. (link, branch 로도 불린다.)
adjacent vertex(인접정점) : 간선에 의해 link된 정점들을 말한다.
degree(차수) : 방향성이 없는 그래프(무방향 그래프)에서 adjacent vertex의 수. (무방향그래프에서, 정점의 모든 degree의 합 = edge의 2배이다.)
in-degree(진입차수) : 방향성이 있는 그래프에서 외부에서 내부로 오는 edge의 수 (내차수라고도 부른다.)
out-degree(진출차수) : 방향성이 있는 그래프에서 내부에서 외부로 향하는 edge의 수 (외차수라고도 한다.)
방향 그래프에서 in-degree + out-degree = edge 이다.
path length(경로길이) : 그래프에서 특정 정점들간의 경로를 구성하는데 사용되는 간선의 수 (위의 그림에서 E와 C간의 path length는 EA, AD, DC 또는 EA, AB, AC로 3이다.)
simple path(단순경로) : 경로 중에 반복되서 지나는 정점이 없는 경우를 말한다.
(참고 : 오일러 경로란 그래프에 존재하는 모든 edge를 한번만 통과해 처음 vertex로 돌아오는 경로(한붓그리기)를 말한다. 모든 vertex에 연결된 edge가 짝수일 때만 오일러 경로가 존재한다고 한다.)
그래프의 종류에는 위의 용어를 설명하면서 언급된 무방향 그래프와 방향 그래프가 있다. 방향성 그래프(바로 아래의 그림 참조)는 방향이 정해져 있는 그래프를 말한다. 방향성 그래프는 edge를 통해서 그래프가 link되어져 있을 때 한쪽 방향에서만 link를 통해 다른 쪽의 vertex를 호출할 수가 있다. 양방향에서 서로 link를 할 수 있는 경우 무방향 그래프라고 한다. 무방향 그래프에는 모든 vertex들 간에 경로가 존재하는 연결 그래프와 그렇지 않은 비연결 그래프가 있다.
( 모든 vertex들이 서로 연결되어 있는 그래프를 완전그래프(complete graph)라고 한다.
이와 같은 경우 모든 vertex 개수 = n 일때, edge의 개수는 n(n-1)/2이다. )

그래프의 종류에는 vertex마다 정보를 담고 있는 가중치 그래프(Weighted Graph, Network(네트워크)라고도 함)이 있다. 각각의 vertex마다 정보가 있어 지도를 표시하거나 지하철노선 및 역정보 등을 설명할 때 등을 표현할 수 있다.
simple path에서 시작 vertex가 끝나는 vertex인 경우 (시작점과 끝점이 같을때) Cycle Graph(순환 그래프)라고 부른다. (아닌 경우는 Acyclic Graph(비순환 그래프)라 한다.)
그래프를 구현하는 방법에는 Adjacency List와 Adjacency Matrix가 있다.

Adjacency List는 adjacent vertex를 list로 나타내는 방법이다.
Graph의 model이 위와 같을 경우, 그림처럼 리스트를 통해 adjacent vertex를 표현할 수가 있다. vertex간의 정보와 edge를 인접리스트에 표현해서 나타내는 방식이다. 이 방식에 경우 Matrix 보다 공간을 덜 차지하지만 상대적으로 보기에 복잡해 보인다.
Adjacency Matrix는 adjacent vertex 를 0과 1을 사용하여 Matrix(배열)로 나타낸 방법이다. Matrix를 통해 나타내면 보기에는 용이하지만 list보다 공간을 많이 차지하게 된다.
그래프를 탐색(search)를 할 때는 일반적으로 DFS(Depth-First Search, 깊이 우선 탐색)와 BFS(Breadth-First Search, 너비 우선 탐색)로 탐색을 한다.
DFS는 vertex에서 다른 vertex로 넘어가 탐색하기 전에 모든 branch를 완벽히 탐색하는 방법이다. 하나하나 세세하게 확인하고 탐색을 진행한는 방법이다.
모든 vertex를 확인하고 싶은 경우에 이 방법을 사용한다.
BFS는 우선적으로 인접한 vertex들을 먼저 탐색하는 방법이다. 넓게 확인하고 그다음 각각의 경로를 확인한다. 특정 경로, 최단 경로 등을 알아내고 싶을 때 이 방법을 선택한다.
(참고 : DFS && BFS
https://www.tutorialspoint.com/data_structures_algorithms/graph_data_structure.htm
https://www.tutorialspoint.com/data_structures_algorithms/breadth_first_traversal.htm )
그래프의 특징에 대해 정리해보면,
Graph Data Structure 는 network model이다.
하나의 vertex에서 2개 이상의 경로가 가능하다.
노드들 사이에서 방향성을 가질 수도 있다.
vertex에서 self-loop외에도 다른 vertex와 loop, circuit이 가능하다.
root node, parent-child라는 개념이 없다. (tree구조와의 차이점)
DFS 또는 BFS 방식으로 순회가 된다.
Graph 는 순환 혹은 비순환이며, 방향성을 가지거나 무방향이다.
간선의 유무 및 개수는 그래프마다, vertex마다 다르다.
'JavaScript' 카테고리의 다른 글
| React, Front-end Library(3) (0) | 2019.11.05 |
|---|---|
| React, Front-end Library(1) (0) | 2019.10.29 |
| Browser, Server, API, HTTP, Ajax (0) | 2019.10.29 |
| Data Structure - Tree , Binary Tree, Binary Searching Tree (0) | 2019.10.29 |
| Data Structure - Stack, Queue, Linked List (0) | 2019.10.29 |




